Applying Artificial Neural Networks (ANNs) for Linear Regression: Yay or Nay?

Did you know that the term “Regression” was first coined by ‘Francis Galton’ in the 19th Century for describing a biological phenomenon?
Regression models have been around for decades.
They have turned out to be extremely useful for providing valuable predictions and modeling real-world problems.
Linear regression, one of the most common and simplest regression models, is useful for determining the relationship between one or more independent variables and a dependent variable.
(Watch our Youtube video on Linear regression by Dr. Ry and get to know all necessary basics).
Whereas, on the other side, artificial neural networks, also referred to as connectionist systems, is a computational model that’s capable of learning new things and making decisions, just like humans.
It’s a component of Artificial Intelligence and has been designed for stimulating the functioning of the human brain.
Regular computers are programmed to behave as if they are interconnected brain cells in order to achieve the goal.
That’s what brings us to our next question,
“Why Should Artificial Neural Networks Be Used For Linear Regression?”
And that’s what we will be taking a look at here.
In this blog post, not only will we take a brief look at each of the concepts, but we will even shift our focus towards the benefits of using artificial neural network for regression as well as some real-life examples.
Well, then!
Let’s dive in.
Fundamentals of Artificial Neural Networks
As we took a look above, an artificial neural network is a piece of a computing system that’s designed for stimulating the manner in which a human brain analyses as well as processes information.
Similar to a human brain, artificial neural networks (ANNs) are built with interconnected nodes, just like a web.
As you might already know, a single human brain consists of innumerable cells referred to as neurons.
Each neuron, made up of a cell body, processes information by carrying it away and towards your brain.
Also called as processing units, an ANN comprises of hundreds or thousands of artificial neurons. Each of these processing units is made up of input as well as output units.
The input ones are subject to receiving different structures and forms of information that are based on an internal weighting system.
In order to produce an output report, the neural network tries to learn about the information.
The set of learning rules followed by ANNs is called as backpropagation.
In the training phase, the ANN tries to recognize the different patterns in the data fed to it. In the supervised phase, the ANN compares the actual output with the desired one in order to detect any differences. These differences are adjusted, as a result of backpropagation.
What this means is that the network operates backward. During both of these stages, the ANN is trained on what exactly it should be looking for as well as what the output looks like. And that’s what makes the network intelligent, which we also call “Deep Learning.”
What Is Linear Regression Exactly?
Linear regression is a commonly-used and basic kind of predictive analysis.
It determines the relationship between one or more independent variables and a dependent variable by simply fitting a linear equation to the observed data.
In simpler terms, this model can help you predict the dependent variable, from one or more independent variables.
Based on your income, a linear regression model can help you predict your expenses. This model can even help you predict Facebook’s revenue, based on its userbase.
Believe me, when I tell you, it’s the simplest model out there that you can easily try out on any data.
Let’s take a look at how you can apply the linear regression model to your own set of data:
- Plot your dependent variable on Y-Axis, against your independent variable on X-Axis
- Plot a straight line
- Measure correlation
- Change the straight line’s direction, until you get the perfect correlation
- Find out the new values on Y-Axis, based on this line
Here’s its equation:
Y=mX+C
- Where Y is a dependent variable
- X is an independent variable
- m is the slope of the line
- C is the intercept
Let’s take into consideration a simple example.
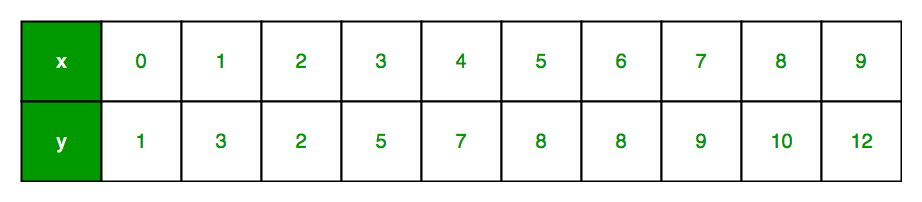
For each value of x, there’s a response y.
Here:
x: Feature vector
y: Response vector
Number of observations (n): 10
Here’s what the scatter plot for the above dataset looks like:
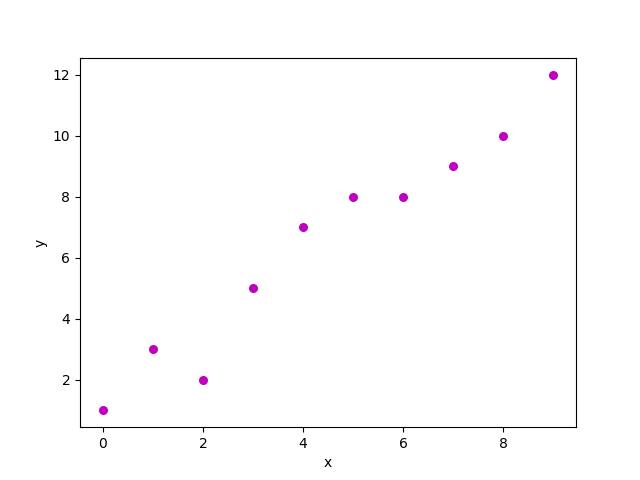
Now, we need to find a line that fits the above scatter-plot perfectly. This line is called the “Regression line.”
The equation for this line is:
Y=mX+C
In order to create the model, we need to estimate or learn the values of m and C. Once we do, we will be able to predict a response.
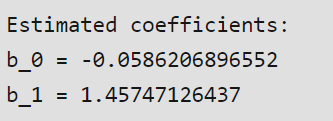
Here, we will be using the “Least Squares Technique.”
Listed below are the values we calculated:
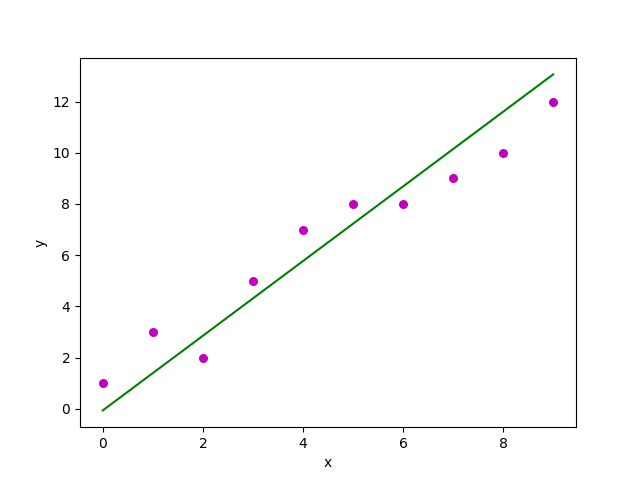
Scatter plot:
Sounds amazing, right?
But the downside to applying the linear regression model is that it’s limited to linear relationships.
This model simply assumes that there’s a linear relationship between the dependent and independent variables. It doesn’t take into consideration other factors.
For instance, the relationship between age and income is curved. During the beginning of your career, you might find your income to below. As you gain experience, your income will begin rising and soon, it will flatten out.
And if we predict your income after you retire, according to the linear regression model, it should be at an all-time high. But that’s not the case. People usually witness a major decline in the income, upon retirement. And that’s the reason you can’t reply to linear regression, in every scenario.
Remember ANNs?
What if I told you that you can use artificial neural network for linear regression?
That’s correct.
Let’s take a look.
Benefits Of Using ANN For Linear Regression
Let’s dive into neural network linear regression basics.
Neural networks can be reduced to regression models.
Well, not exactly “reduced.” But, a neural network can easily “pretend” to act as any kind of regression model.
Let’s take a look at why you should use ANN for linear regression.
Ability To Learn & Model Linear & Non-Linear Relationships
One of the downsides of the Linear regression model that we took a look at above is that it assumes that there’s always a linear relationship between the dependent as well as independent variables.
What if it’s curved?
What if this model showed you a huge boost in your income after you retire? That’d be pretty disappointing, right?
And one of the biggest benefits of using ANNs for linear regression is that it takes into account the real-life relationships as well.
It’s able to adapt to linear as well as non-linear models, depending on how it has been trained.
It’s a flexible model that can easily adapt to the shape of the data. And if the results aren’t accurate enough, you can easily add further hidden neuron layers in order to improve its prediction capabilities and turn it more complex.
Fault-Tolerant
What if one or multiple cells of the ANN have been corrupted?
Will it stop working entirely?
That’d be a disaster, right?
But the thing is an artificial neural network is fault-tolerant. No matter what the situation is, it will always provide you with output.
Will Perform Gradient Descent
ANNs will never stop learning. After the training process, ANNs will be performing gradient descent in order to find even better-fitting coefficients that fit the data accurately.
“Gradient descent is a mathematical technique that plays a role in modifying a function’s parameters to decline from a higher-value to a lower value of a function. It does so by analyzing the derivatives of a function, on the basis of each of the parameters, and by learning about the next best step for minimizing the function. Applying it to the error function will result in the discovery of the weights with lower error values, thereby playing a role in turning the entire model perfect.”
ANNs will continue doing so until the model arrives at the most favorable linear regression coefficients.
Let’s learn how you can apply ANNs to Linear Regression problems.
3 Examples Of How To Apply Artificial Neural Network For Linear Regression
Listed below are the neural network regression examples we’ll be taking a look at:
- Linear Regression Using Tensorflow
- Linear Regression Using PyTorch
- Linear Regression Using Theano
Linear Regression Using Tensorflow
Let’s look at Tensorflow linear regression example. You need to complete a few steps.
- Import all the 3 libraries.

- For making the random numbers unpredictable, we’ll be defining fixed seeds for Tensorflow as well as Numpy.

- The above-mentioned steps will help you generate random data.

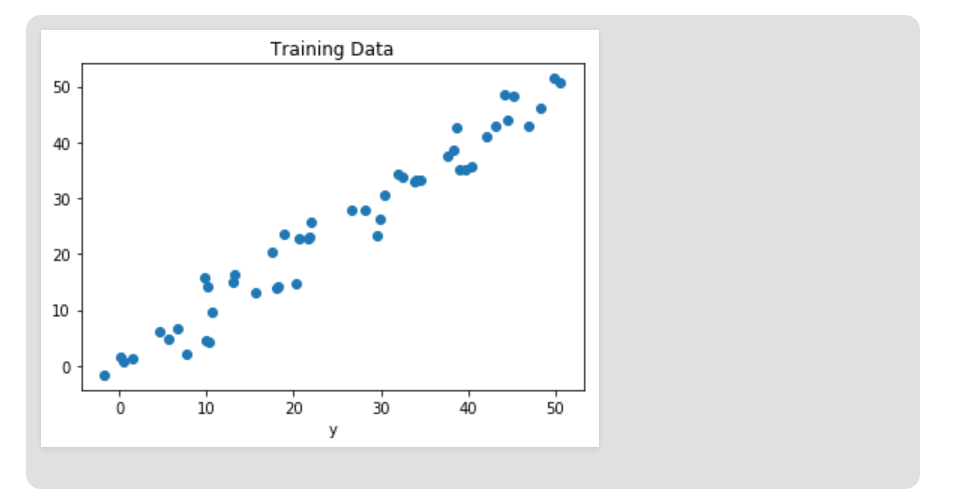
- Now, we will be visualizing the training data.

- The output will be:
- Define the placeholders for x & y

- Define 2 trainable Tensorflow variables for bias and weights. np.random.randn() will initialize them randomly.

- Define model’s hyperparameters: Number of Epochs & the Learning Rate

- Build the cost optimizer, cost function, and the hypothesis. We are not going to implement the Gradient Descent Optimizer manually. That’s because it’s in-built. Now, it’s time to initialize the variables.

- Let’s begin with training the model.
- Output:
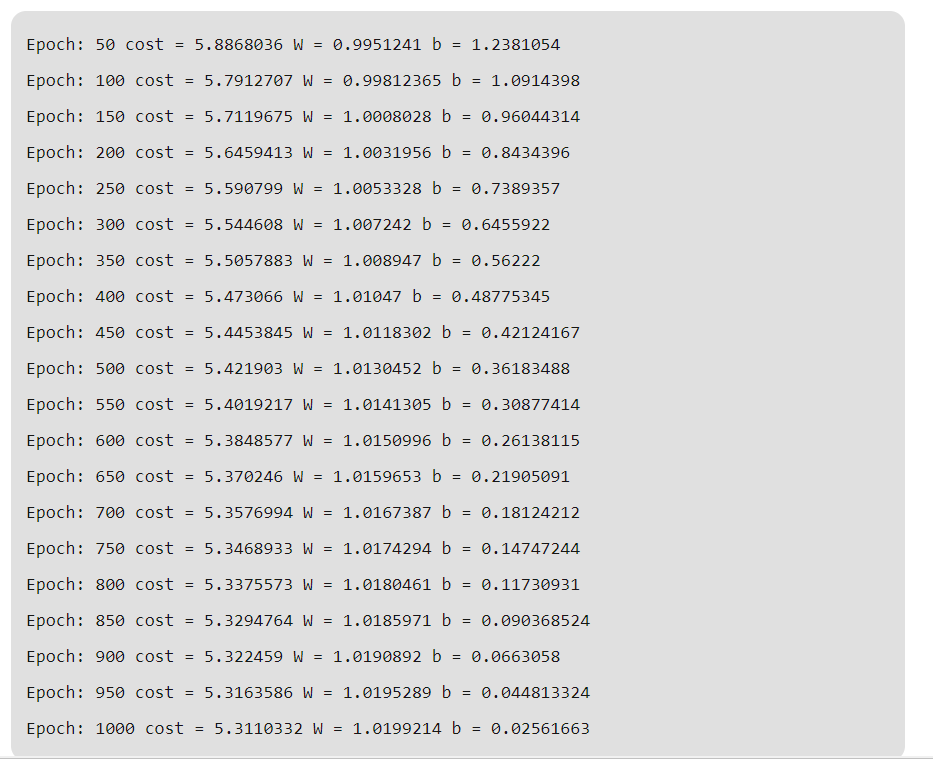
- Let us analyze the result of linear regression using Tensorflow

- Output:

- Remember that both bias and weight are scalars. Let’s plot the result.

- Output:
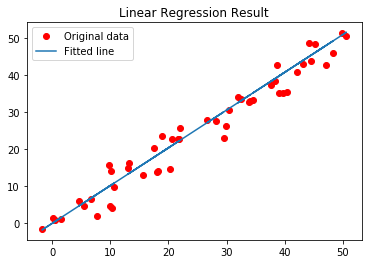
Ladies & Gentlemen, that’s how linear regression at Tensorflow works.
Now, let’s take at another example using PyTorch.
Linear Regression Using PyTorch
This time let’s see a linear regression PyTorch example.
- First of all, if you don’t have PyTorch installed, it’s time you headed over to pytorch.org.
- Once you do, begin by importing the required objects and library functions

- Define some data. Assign them to x_data and y_data variables

- x_data -> Independent Variable & y_data -> dependent variable. Now, it’s time to define the model. Listed below are the two most vital steps:
- Initializing the model
- Declaring forward pass
- Here’s the class we’ll be using:

- The model class is the subclass of torch.nn.module. We’ve 1 input as well as 1 output. Let’s now create an object.

- Now, select the loss criteria and optimizer. We’ll be using Mean Squared Error as loss function & stochastic gradient descent as the optimizer. Let’s fix the learning rate as 0.01

- Now, it’s time to train the model

- Once the training phase is completed successfully, we’ll be testing whether the results are correct or not.

- If all of the above-mentioned steps were correctly performed, you’d get the value somewhere close to 8 for input 4.0. Here’s what we got:
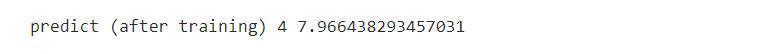
Ladies & Gentlemen, that’s how you can use PyTorch linear regression.
Linear Regression Using Theano
The last example is neural networks for regression using Theano.
- Import the mandatory library functions and the training data
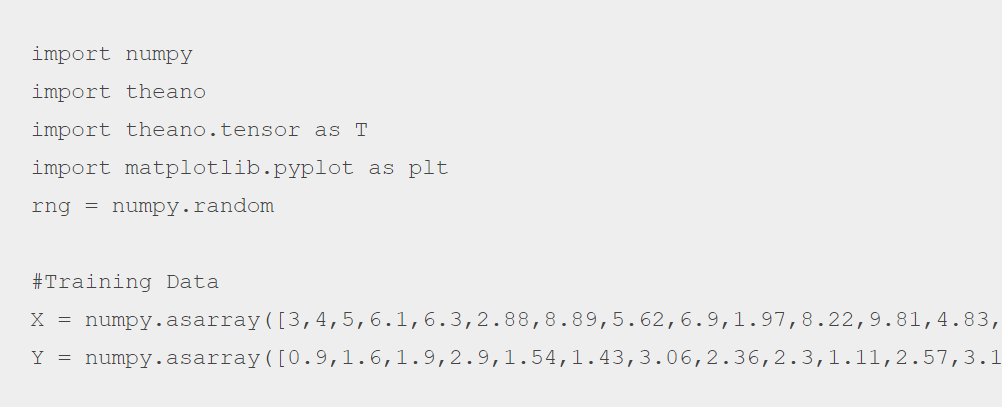
- Now, we will randomly initialize the coefficients, i.e. m & c as shared variables. That’s because they will be extensively used during the entire process.
- Now let’s define x and y as symbolic variables. These differ from the ones we are used to in Python. These help Theano achieve outstanding computation speeds.

- Define cost function: It’s the cumulative error that will be predicted by the model for the current coefficients. During the entire process, the model will be trying to minimize the cost function to better fit the training data. Here, we will be considering cumulative MSE of the predicted value as well as the true value as a cost parameter

- Now, we will be multiplying the input values by slope m and adding intercept c in order to get the predicted value. Once you calculate the cost factor, it’s time, to begin with, the optimization process. Here the learning rate will be 0.01 and the training frequency will be 10000.
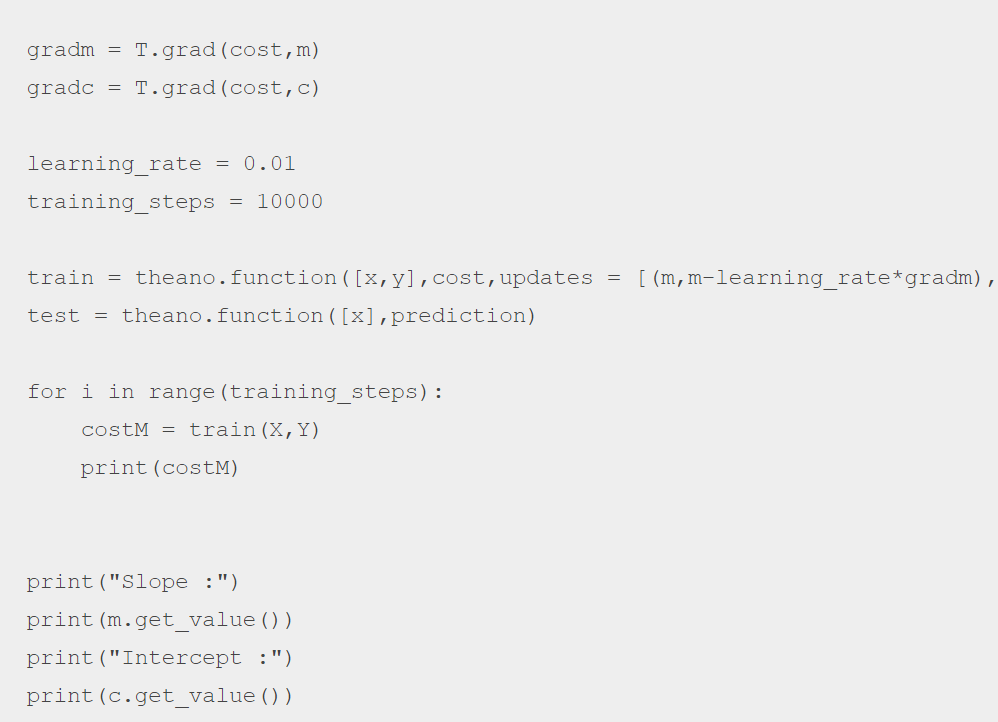
- Here’s the final predicted model that you’ll get:
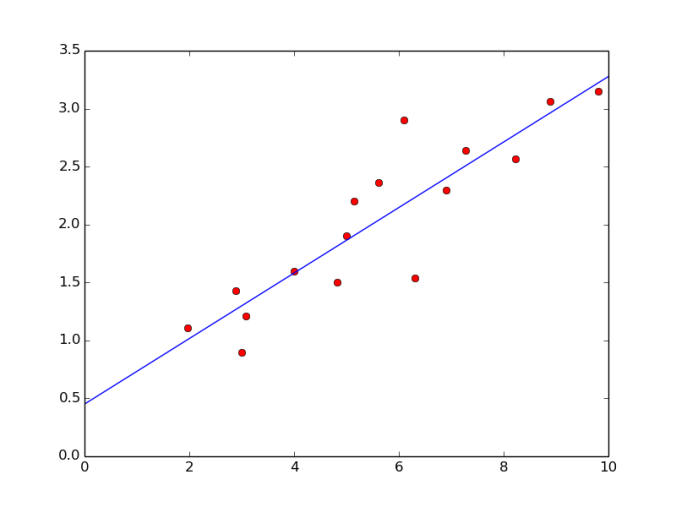
Conclusion
Congratulations! You have successfully uncovered the secret of using ANNs for linear regression. Also you’ve got familiar with neural network regression examples. Good job!
In order to run neural network for regression, you will have to utilize one of the frameworks we mentioned above. There are various other. But, these 3 are my personal favorite. I’ve rarely seen a regression equation perfectly fitting all of the expected datasets.





